Interval Of Convergence Ratio Test

Domain of convergence of power series

In mathematics, the radius of convergence of a power series is the radius of the largest deejay at the center of the series in which the series converges. Information technology is either a non-negative real number or ${\displaystyle \infty }$ . When it is positive, the ability series converges admittedly and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic role to which it converges. In case of multiple singularities of a function (singularities are those values of the argument for which the function is non divers), the radius of convergence is the shortest or minimum of all the corresponding distances (which are all non-negative numbers) calculated from the heart of the deejay of convergence to the respective singularities of the function.

Definition [edit]

For a power series f defined as:

${\displaystyle f(z)=\sum _{n=0}^{\infty }c_{due north}(z-a)^{north},}$

where

• a is a circuitous constant, the middle of the disk of convergence,
• c _{due north} is the due north-th complex coefficient, and
• z is a complex variable.

The radius of convergence r is a nonnegative existent number or ${\displaystyle \infty }$ such that the series converges if

${\displaystyle |z-a|<r}$

and diverges if

${\displaystyle |z-a|>r.}$

Some may prefer an alternative definition, as being is obvious:

${\displaystyle r=\sup \left\{|z-a|\ \left|\ \sum _{northward=0}^{\infty }c_{n}(z-a)^{n}\ {\text{ converges }}\right.\correct\}}$

On the purlieus, that is, where |z −a| = r, the behavior of the power series may be complicated, and the series may converge for some values of z and diverge for others. The radius of convergence is infinite if the series converges for all complex numbers z.^[1]

Finding the radius of convergence [edit]

Two cases arise. The showtime case is theoretical: when y'all know all the coefficients ${\displaystyle c_{due north}}$ and so y'all accept sure limits and find the precise radius of convergence. The second case is applied: when you construct a ability series solution of a difficult problem you typically will but know a finite number of terms in a power series, anywhere from a couple of terms to a hundred terms. In this 2d case, extrapolating a plot estimates the radius of convergence.

Theoretical radius [edit]

The radius of convergence can be institute past applying the root examination to the terms of the serial. The root test uses the number

${\displaystyle C=\limsup _{n\to \infty }{\sqrt[{n}]{|c_{n}(z-a)^{north}|}}=\limsup _{n\to \infty }\left({\sqrt[{n}]{|c_{northward}|}}\right)|z-a|}$

"lim sup" denotes the limit superior. The root test states that the serial converges if C < i and diverges ifC > 1. It follows that the ability serial converges if the distance from z to the center a is less than

${\displaystyle r={\frac {1}{\limsup _{n\to \infty }{\sqrt[{n}]{|c_{n}|}}}}}$

and diverges if the distance exceeds that number; this statement is the Cauchy–Hadamard theorem. Note that r = one/0 is interpreted as an infinite radius, meaning that f is an entire function.

The limit involved in the ratio test is unremarkably easier to compute, and when that limit exists, it shows that the radius of convergence is finite.

${\displaystyle r=\lim _{due north\to \infty }\left|{\frac {c_{north}}{c_{n+1}}}\right|.}$

This is shown every bit follows. The ratio test says the series converges if

${\displaystyle \lim _{n\to \infty }{\frac {|c_{northward+1}(z-a)^{n+ane}|}{|c_{n}(z-a)^{north}|}}<1.}$

That is equivalent to

${\displaystyle |z-a|<{\frac {1}{\lim _{n\to \infty }{\frac {|c_{n+1}|}{|c_{n}|}}}}=\lim _{n\to \infty }\left|{\frac {c_{n}}{c_{northward+1}}}\right|.}$

Practical estimation of radius in the instance of real coefficients [edit]

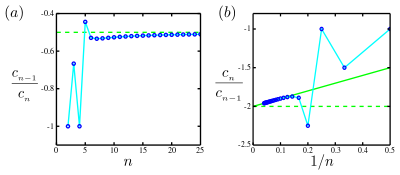
Plots of the function ${\displaystyle f(\varepsilon )={\frac {\varepsilon (i+\varepsilon ^{iii})}{\sqrt {i+2\varepsilon }}}.}$
The solid green line is the straight-line asymptote in the Domb–Sykes plot,^[ii] plot (b), which intercepts the vertical axis at −2 and has a gradient +1. Thus there is a singularity at ${\displaystyle \varepsilon =-one/ii}$ and and then the radius of convergence is ${\displaystyle r=i/2.}$

Ordinarily, in scientific applications, but a finite number of coefficients ${\displaystyle c_{n}}$ are known. Typically,^{[ vague ]} every bit ${\displaystyle n}$ increases, these coefficients settle into a regular behavior determined by the nearest radius-limiting singularity. In this example, ii principal techniques accept been adult, based on the fact that the coefficients of a Taylor serial are roughly exponential with ratio ${\displaystyle 1/r}$ where r is the radius of convergence.

• The basic case is when the coefficients ultimately share a common sign or alternate in sign. As pointed out earlier in the commodity, in many cases the limit ${\textstyle \lim _{n\to \infty }{c_{northward}/c_{n-1}}}$ exists, and in this case ${\textstyle 1/r=\lim _{due north\to \infty }{c_{n}/c_{n-one}}}$ . Negative ${\displaystyle r}$ ways the convergence-limiting singularity is on the negative centrality. Judge this limit, by plotting the ${\displaystyle c_{n}/c_{n-one}}$ versus ${\displaystyle 1/n}$ , and graphically extrapolate to ${\displaystyle 1/n=0}$ (effectively ${\displaystyle n=\infty }$ ) via a linear fit. The intercept with ${\displaystyle 1/n=0}$ estimates the reciprocal of the radius of convergence, ${\displaystyle i/r}$ . This plot is chosen a Domb–Sykes plot.^[3]
• The more complicated case is when the signs of the coefficients have a more complex pattern. Mercer and Roberts proposed the following procedure.^[four] Define the associated sequence

  $${\displaystyle b_{n}^{two}={\frac {c_{n+1}c_{n-1}-c_{n}^{2}}{c_{n}c_{n-2}-c_{n-one}^{2}}}\quad n=3,4,v,\ldots .}$$

  

  Plot the finitely many known ${\displaystyle b_{northward}}$ versus ${\displaystyle 1/n}$ , and graphically extrapolate to ${\displaystyle 1/n=0}$ via a linear fit. The intercept with ${\displaystyle ane/due north=0}$ estimates the reciprocal of the radius of convergence, ${\displaystyle 1/r}$ . This process also estimates two other characteristics of the convergence limiting singularity. Suppose the nearest singularity is of degree ${\displaystyle p}$ and has angle ${\displaystyle \pm \theta }$ to the existent centrality. And so the slope of the linear fit given in a higher place is ${\displaystyle -(p+1)/r}$ . Further, plot ${\textstyle {\frac {1}{two}}\left({\frac {c_{n-1}b_{n}}{c_{due north}}}+{\frac {c_{northward+1}}{c_{n}b_{n}}}\correct)}$ versus ${\textstyle ane/n^{ii}}$ , then a linear fit extrapolated to ${\textstyle 1/n^{2}=0}$ has intercept at ${\displaystyle \cos \theta }$ .

Radius of convergence in complex assay [edit]

A power series with a positive radius of convergence can be made into a holomorphic function by taking its argument to be a circuitous variable. The radius of convergence can exist characterized by the following theorem:

The radius of convergence of a power serial f centered on a point a is equal to the altitude from a to the nearest bespeak where f cannot be defined in a way that makes information technology holomorphic.

The ready of all points whose altitude to a is strictly less than the radius of convergence is called the deejay of convergence.

A graph of the functions explained in the text: Approximations in bluish, circle of convergence in white

The nearest point means the nearest betoken in the complex airplane, not necessarily on the existent line, fifty-fifty if the center and all coefficients are real. For case, the function

${\displaystyle f(z)={\frac {1}{1+z^{2}}}}$

has no singularities on the existent line, since ${\displaystyle 1+z^{two}}$ has no real roots. Its Taylor series nearly 0 is given by

${\displaystyle \sum _{n=0}^{\infty }(-i)^{n}z^{2n}.}$

The root exam shows that its radius of convergence is 1. In accordance with this, the role f(z) has singularities at ±i, which are at a altitude 1 from 0.

For a proof of this theorem, see analyticity of holomorphic functions.

A simple case [edit]

The arctangent function of trigonometry tin can exist expanded in a power series:

${\displaystyle \arctan(z)=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{seven}}{seven}}+\cdots .}$

It is piece of cake to use the root examination in this case to find that the radius of convergence is 1.

A more complicated example [edit]

Consider this power series:

${\displaystyle {\frac {z}{e^{z}-1}}=\sum _{north=0}^{\infty }{\frac {B_{n}}{n!}}z^{n}}$

where the rational numbers B _northward are the Bernoulli numbers. Information technology may be cumbersome to endeavour to employ the ratio test to detect the radius of convergence of this series. But the theorem of circuitous assay stated above apace solves the problem. At z = 0, at that place is in outcome no singularity since the singularity is removable. The merely non-removable singularities are therefore located at the other points where the denominator is zero. We solve

${\displaystyle e^{z}-one=0}$

past recalling that if z = x + iy and e ^iy = cos(y) + i sin(y) then

${\displaystyle east^{z}=due east^{x}e^{iy}=e^{x}(\cos(y)+i\sin(y)),}$

and and then accept ten and y to be existent. Since y is real, the absolute value of cos(y) + i sin(y) is necessarily one. Therefore, the absolute value of eastward ^z can be i only if e ^ten is ane; since x is real, that happens only if x = 0. Therefore z is purely imaginary and cos(y) + i sin(y) = i. Since y is real, that happens simply if cos(y) = i and sin(y) = 0, so that y is an integer multiple of 2π. Consequently the singular points of this function occur at

z = a nonzero integer multiple of 2π i.

The singularities nearest 0, which is the center of the ability series expansion, are at ±2π i. The distance from the centre to either of those points is 2π, so the radius of convergence is 2π.

Convergence on the purlieus [edit]

If the ability series is expanded around the point a and the radius of convergence is r , then the set of all points z such that | z − a | = r is a circle called the purlieus of the disk of convergence. A power series may diverge at every point on the boundary, or diverge on some points and converge at other points, or converge at all the points on the boundary. Furthermore, even if the series converges everywhere on the boundary (fifty-fifty uniformly), it does not necessarily converge absolutely.

Case one: The power series for the function f(z) = 1/(i − z), expanded around z = 0, which is just

${\displaystyle \sum _{n=0}^{\infty }z^{n},}$

has radius of convergence 1 and diverges at every point on the boundary.

Example ii: The power series for g(z) = −ln(1 − z), expanded around z = 0, which is

${\displaystyle \sum _{north=i}^{\infty }{\frac {one}{n}}z^{n},}$

has radius of convergence ane, and diverges for z = one simply converges for all other points on the purlieus. The function f(z) of Instance 1 is the derivative of g(z).

Instance three: The power series

${\displaystyle \sum _{northward=1}^{\infty }{\frac {1}{northward^{ii}}}z^{n}}$

has radius of convergence 1 and converges everywhere on the boundary admittedly. If h is the function represented by this series on the unit disk, then the derivative of h(z) is equal to g(z)/z with g of Example ii. It turns out that h(z) is the dilogarithm part.

Instance iv: The ability serial

${\displaystyle \sum _{i=ane}^{\infty }a_{i}z^{i}{\text{ where }}a_{i}={\frac {(-i)^{northward-one}}{ii^{due north}n}}{\text{ for }}n=\lfloor \log _{ii}(i)\rfloor +1{\text{, the unique integer with }}2^{northward-1}\leq i<2^{north},}$

has radius of convergence 1 and converges uniformly on the unabridged boundary | z | = 1, but does not converge absolutely on the purlieus.^[five]

Rate of convergence [edit]

If nosotros aggrandize the function

${\displaystyle \sin x=\sum _{north=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+one}=x-{\frac {x^{3}}{3!}}+{\frac {ten^{5}}{five!}}-\cdots {\text{ for all }}x}$

around the point 10 = 0, we observe out that the radius of convergence of this series is ${\displaystyle \infty }$ meaning that this series converges for all circuitous numbers. However, in applications, 1 is often interested in the precision of a numerical answer. Both the number of terms and the value at which the series is to exist evaluated bear upon the accuracy of the answer. For example, if nosotros want to calculate sin(0.1) accurate up to five decimal places, we but demand the start two terms of the series. Yet, if we desire the same precision for 10 = 1 we must evaluate and sum the outset five terms of the series. For sin(10), one requires the first 18 terms of the series, and for sin(100) we demand to evaluate the first 141 terms.

So for these particular values the fastest convergence of a power serial expansion is at the eye, and as one moves away from the center of convergence, the rate of convergence slows downward until you attain the boundary (if it exists) and cross over, in which case the serial will diverge.

Abscissa of convergence of a Dirichlet serial [edit]

An analogous concept is the abscissa of convergence of a Dirichlet serial

${\displaystyle \sum _{due north=1}^{\infty }{\frac {a_{n}}{n^{south}}}.}$

Such a series converges if the real role of southward is greater than a particular number depending on the coefficients a _northward : the abscissa of convergence.

Notes [edit]

1. ^ Mathematical Analysis-II. Krishna Prakashan Media. 16 November 2010.
2. ^ Run across Effigy 8.1 in: Hinch, E.J. (1991), Perturbation Methods, Cambridge Texts in Applied Mathematics, vol. 6, Cambridge University Press, p. 146, ISBN0-521-37897-4
3. ^ Domb, C.; Sykes, Chiliad.F. (1957), "On the susceptibility of a ferromagnetic in a higher place the Curie point", Proc. R. Soc. Lond. A, 240 (1221): 214–228, Bibcode:1957RSPSA.240..214D, doi:10.1098/rspa.1957.0078, S2CID 119974403
4. ^ Mercer, G.Northward.; Roberts, A.J. (1990), "A middle manifold description of contaminant dispersion in channels with varying flow properties", SIAM J. Appl. Math., 50 (6): 1547–1565, doi:10.1137/0150091
5. ^ Sierpiński, W. (1918). "O szeregu potęgowym, który jest zbieżny na całem swem kole zbieżności jednostajnie, ale nie bezwzględnie". Prace Matematyczno-Fizyczne. 29 (1): 263–266.

References [edit]

• Brown, James; Churchill, Ruel (1989), Circuitous variables and applications, New York: McGraw-Hill, ISBN978-0-07-010905-6
• Stein, Elias; Shakarchi, Rami (2003), Circuitous Assay, Princeton, New Jersey: Princeton University Press, ISBN0-691-11385-8

See too [edit]

• Abel's theorem
• Convergence tests
• Root test

External links [edit]

• What is radius of convergence?

Interval Of Convergence Ratio Test,

Source: https://en.wikipedia.org/wiki/Radius_of_convergence

Posted by: thorntontheinglee.blogspot.com

Share this post